Masked Vision Transformers for Hyperspectral Image Classification
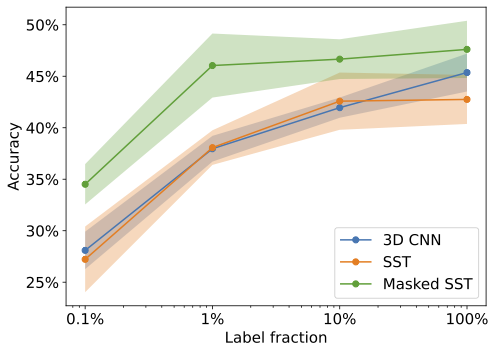
Transformer architectures have become state-of-the-art models in computer vision and natural language processing. To a significant degree, their success can be attributed to self-supervised pre-training on large scale unlabeled datasets. This work investigates the use of self-supervised masked image reconstruction to advance transformer models for hyperspectral remote sensing imagery. To facilitate self-supervised pre-training, we build a large dataset of unlabeled hyperspectral observations from the EnMAP satellite and systematically investigate modifications of the vision transformer architecture to optimally leverage the characteristics of hyperspectral data. We find significant improvements in accuracy on different land cover classification tasks over both standard vision and sequence transformers using (i) blockwise patch embeddings, (ii) spatial-spectral self-attention, (iii) spectral positional embeddings and (iv) masked self-supervised pre-training (Code available at github.com/HSG-AIML/MaskedSST). The resulting model outperforms standard transformer architectures by +5% accuracy on a labeled subset of our EnMAP data and by +15% on Houston2018 hyperspectral dataset, making it competitive with a strong 3D convolutional neural network baseline. In an ablation study on label-efficiency based on the Houston2018 dataset, self-supervised pre-training significantly improves transformer accuracy when little labeled training data is available. The self-supervised model outperforms randomly initialized transformers and the 3D convolutional neural network by +7-8% when only 0.1-10% of the training labels are available.
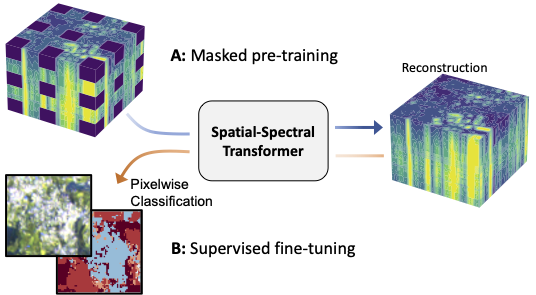
Our work adapts the transformer architecture for hyperspectral data. We apply self-attention across the spatial and spectral dimensions by factorizing the transformer. Additionally, we utilize spectral positional embeddings together with an initial block-wise patch-embedding layer. The resulting spatial-spectral transformer is pre-trained with a masked image modeling objective on a large collection of hyperspectral remote sensing data from the EnMAP satellite. Downstream performance is evaluated on two datasets: the Houston2018 hyperspectral scene, and a land-cover task based on EnMAP hyperspectral data and DFC2020 labels in Mexico City.

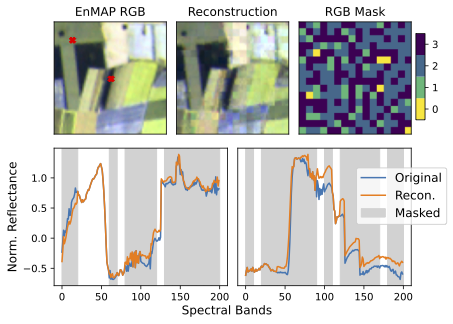
Our results show that unsupervised pre-training with a mask image modeling objective improves downstream hyperspectral image classification performance.
Moreover, we are able to show the efficiency of pre-training with our approach: with only 1% of the labelled data, the supervised spatial-spectral transformer outperforms baselines trained trained on the entire dataset. The performance rapidly increases with the amount of available labelled training data for all models.

To conclude, our approach illustrates the utility of Transformer models for hyperspectral remote sensing image classification.
The results of this study have been presented at the CVPR 2023 EarthVision workshop in Vancouver, Canada.