NeurIPS 2022 - Model Zoo Datasets and Generative Hyper-Representations
Introduction
Learning on populations of Neural Networks (NNs) has become an emerging topic in recent years.
The high dimensionality, non-linearity and non-convexity of NN training opens up exciting research questions investigating populations:
i) do individual models in populations have something in common?
ii) do models form meaningful structures in weight space?
iii) can representations be learned of such structures?
iv) can such structures be exploited to generate new models?
At last year’s NeurIPS, we took first steps to find answers to these questions with our paper presenting hyper-representations.
There, we showed that populations of models, called model zoos, are indeed structured. With hyper-representations, we proposed a self-supervised learning method to learn
representations of the weights of model zoos. Further, we showed that these representations are meaningful in the sense that they are predictive of model properties,
such as their accuracy, epoch or hyperparamters.
At this year’s NeurIPS, two more contributions in this research direction got accepted: 1) the Model Zoo Dataset to facilitate research in that domain; and 2) Generative Hyper Representations to sample new NN weights.
Model Zoo Dataset
Link: https://modelzoos.cc
Paper: https://arxiv.org/abs/2209.14764
Talk: https://neurips.cc/virtual/2022/poster/55727
Background
Research on populations of Neural Networks requires access to such populations. While collections of models exist (i.e., model hubs like huggingface), they are usually unstructured, often small or contain only a small degree of diversity. For our own reserach and to facilitate reserach on model populations for the community at large, we therefore generated large, structured and diverse populations. The model zoos are an open source blueprint, so that they can be replicated, changed or extended to fit the community needs.
Dataset Generation
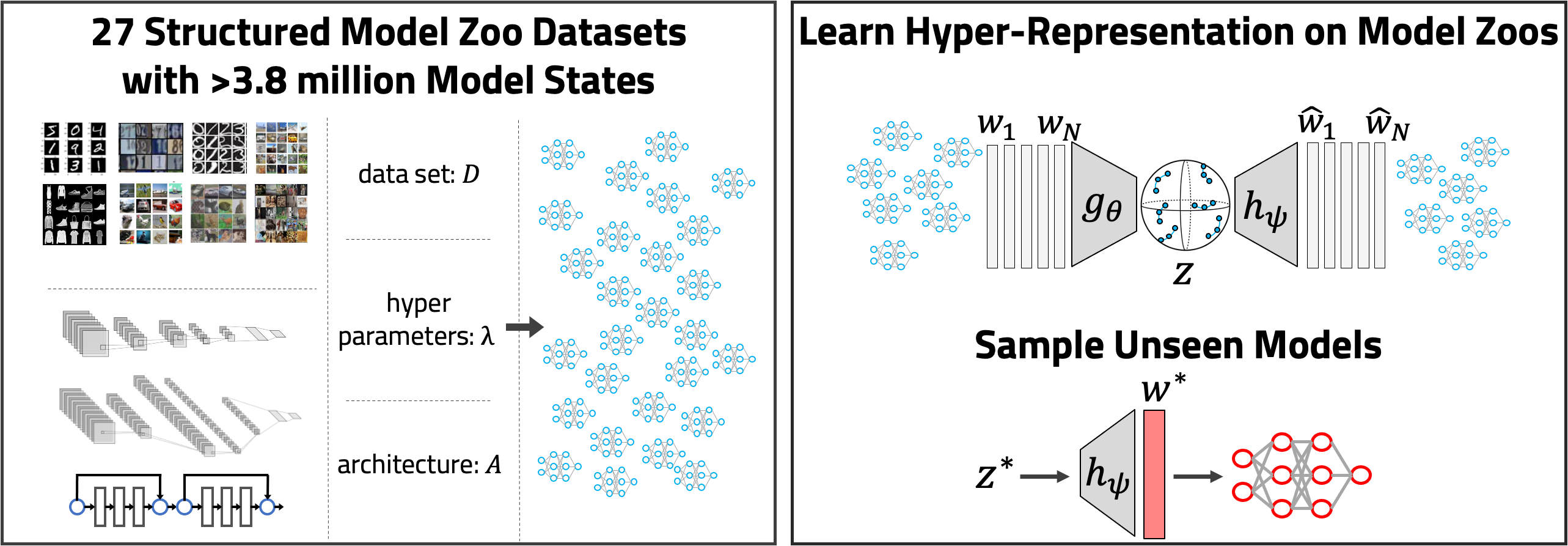
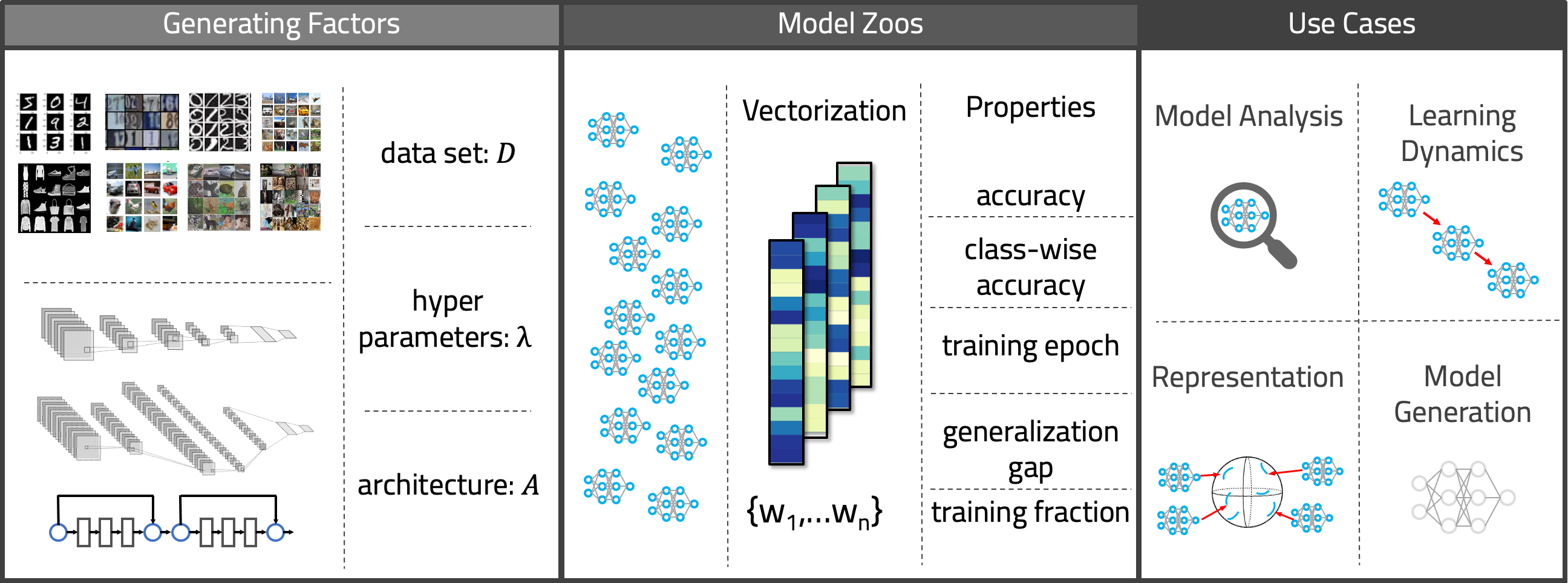
All in all, there are (as of now) 27 model zoos, with 50’360 unique Neural Network models and over 3.8 Million model states.
The zoos are trained on 8 computer vision datasets (MNIST, F-MNIST, SVHN, USPS, STL, CIFAR10, CIFAR100, Tiny ImageNet),
using 3 architectures (small CNN, medium CNN and ResNet-18).
To include different types of diversity, we vary different hyperparameters for different zoos. In some, we vary only the random seed, in others also the initialization method, activation function, optimizer, learning rate, weight decay and dropout.
As sparsification has not yet been studied on a population level, we also include sparsified model zoo twins, for which all models in a zoo at their last epoch are iteratively sparsified with Variational Dropout (VD).
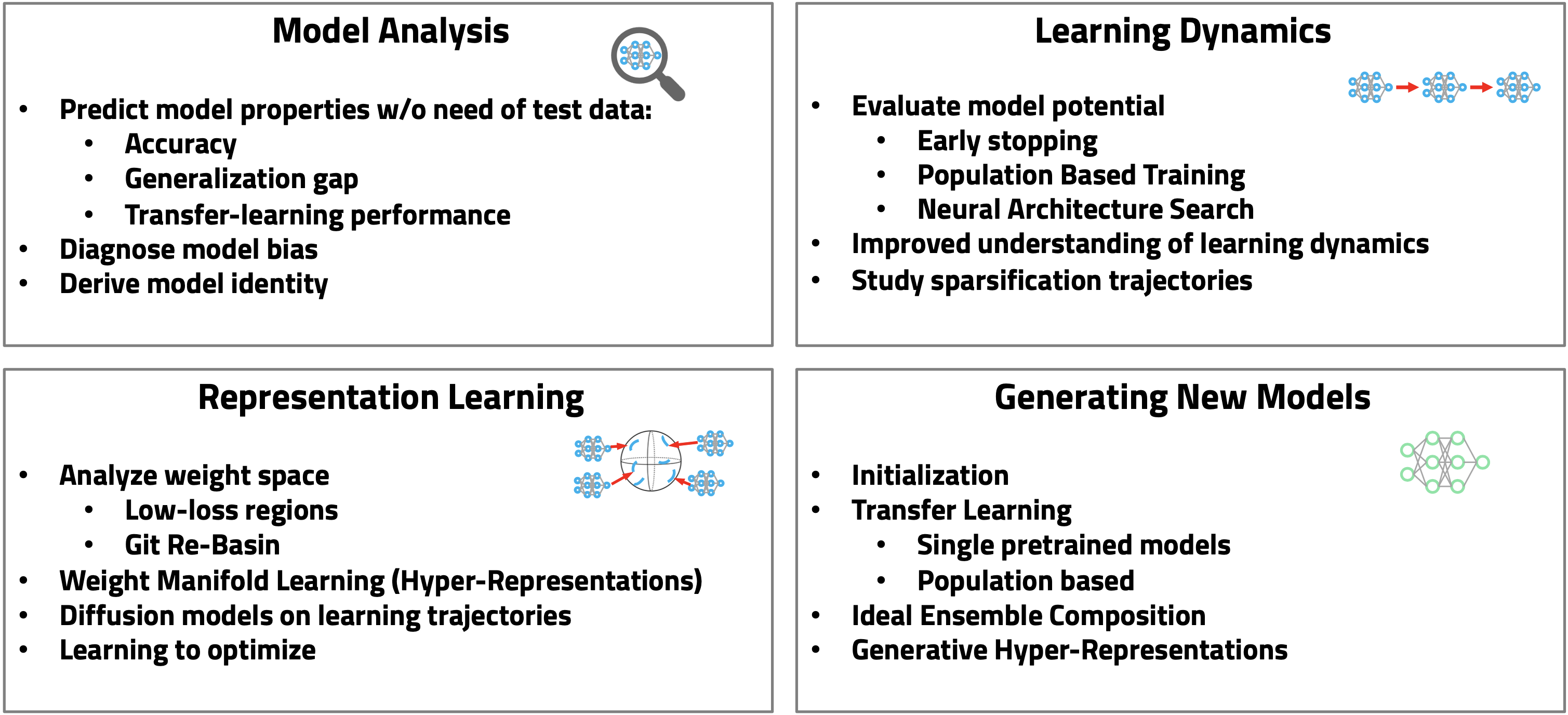
Potential Use-Cases
As the domain of model populations is still somewhat new, we also consider potential use-cases for model populations. They include model analysis, i.e., the prediction of model properties based on populations, where already some work has been done. Similarly, populations could be used to investigate the learning dynamics of models further, and extend methods like Population Based Training. Model zoos can further be used as datasets for representation learning, as in our hyper-representations. Lastly, such populations may allow to systematically study how to generate weights, as good initializations or for transfer learning.
Hyper-Representations as Generative Models: Sampling Unseen Neural Network Weights
Paper: https://arxiv.org/abs/2209.14733
Talk: https://neurips.cc/virtual/2022/poster/53429
Code: https://github.com/HSG-AIML/NeurIPS_2022-Generative_Hyper_Representations
Background
In previous work, we showed that hyper-representations embed populations of models in a meaningful way, i.e., disentangling latent properties such as accuracy, or training progress. For this project, we therefore investigated if such hyper-representations can be leveraged to generate new models with targeted properties.
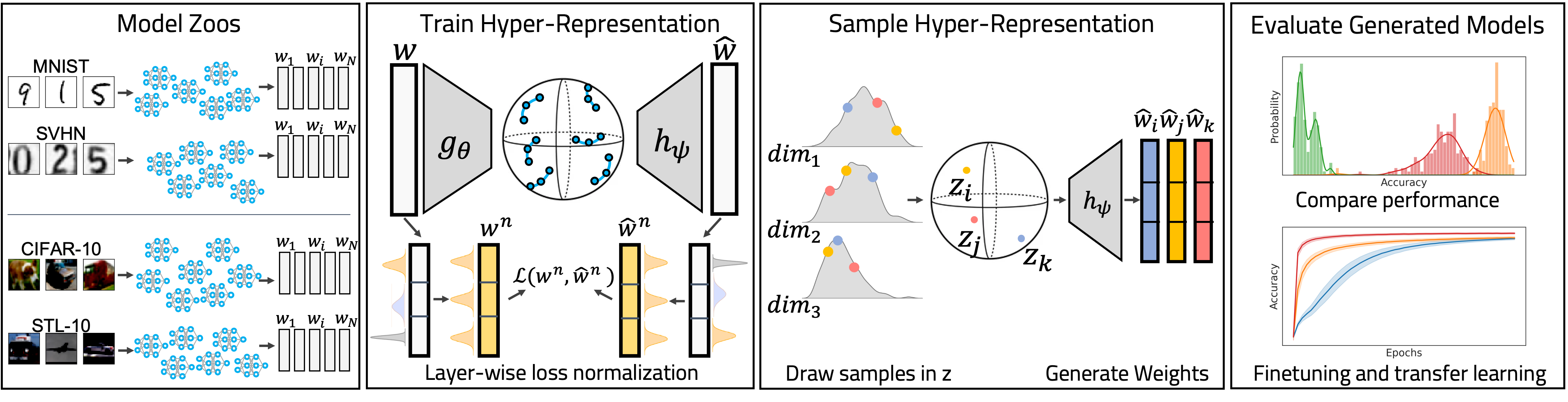
Approach
The approach is split in two parts: i) training hyper-representations and ii) sampling hyper-representations. In our experiments, we noticed that weight distributions often vary over the layers. That causes the loss contribution and thus reconstruction quality to be unequally distributed and results in poor model performance. To fix that, we introduce a layer-wise loss normalization, which improves the reconstruction of weights of all layers and drastically improves model accuracy, see Figure below.
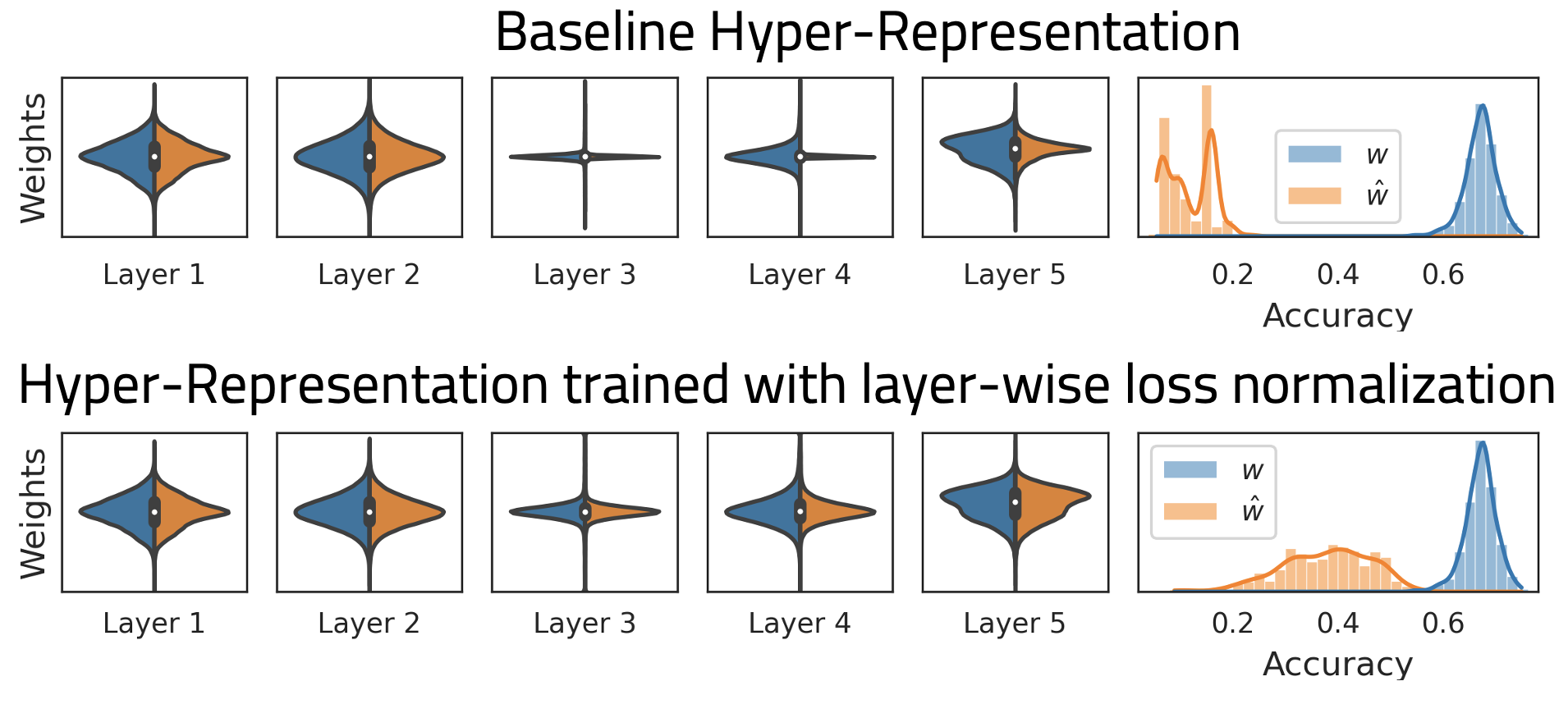
From such hyper-representations, we can now draw samples and decode them to weights. Previous work has shown that hyper-representations disentangle model accuracy, so that sampling can target high accuracy models. Unfortunately, the representation space is still relatively high dimensional, so that simply sampling the joint distribution is infeasible. To deal with that, we propose three sampling methods: i) by assuming conditional independence, sampling from the distribution per latent dimension; ii) based on the neighborhood, which is mapped approximately to a lower dimension; and iii) by using a GAN. The sampled hyper-representations are then decoded to weights and loaded in models.
Results
We evaluate the generated weights by comparing their accuracy, in fine-tuning and transfer learning experiments as well as ensembles.
First, we find that the sampling methods are specific: the choice of sampling method determines the accuracy bracket in which the sampled models end up in.
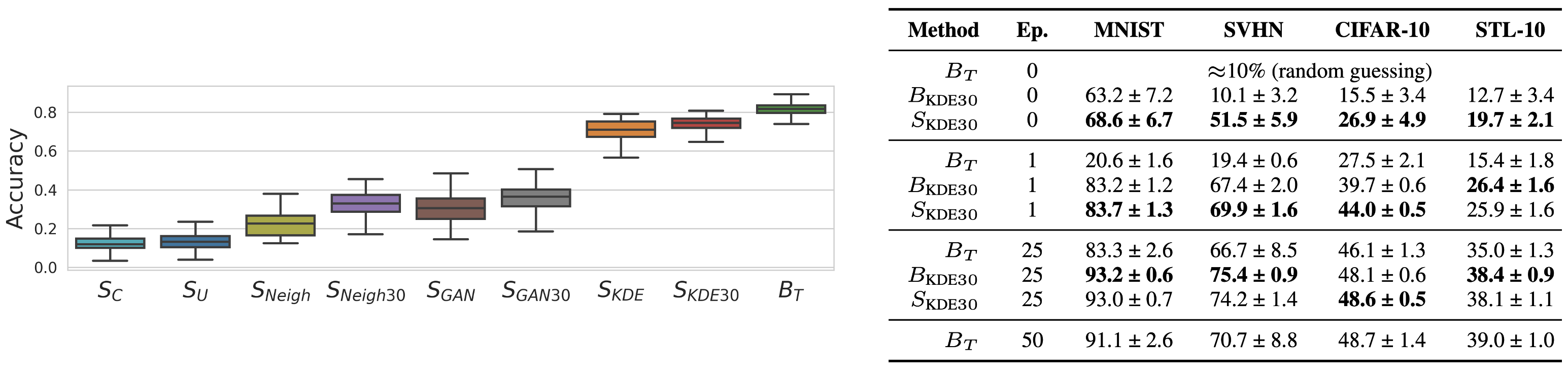
Further, we find that sampled models outperform or at least match the baselines in fine-tuning. In other words: samples drawn from hyper-representations often achieve higher performance than the models in the zoo on which the hyper-representation was trained.
However, we were curious if hyper-representations generalize beyond their task and architecture. Surprisingly, they do. In a transfer-learning setup, sampled weights outperform or match strong baselines. What is more, the generated weights generalize even to architecture changes and outperform training from scratch by a large margin.

Conclusion
The two contributions provide large and diverse datasets for research on model populations as well as new methods to generate neural network models. They provide grounds for many more research projects, to which we invite the community to join in.