The parameters of Neural Networks (NNs) develop on smooth, unique trajectories during training. Using clustering methods in parameter space, these trajectories can be recovered without labels, and even the order of checkpoints on the trajectories restored to some degree. We hypothesise that the shape of the trajectories contains information on the training progress, and may reveal domain shifts in the training data or adversarial attacks. Therefore, training trajectories may be used for monitoring of the training progress, and supply useful information for NN model versioning.

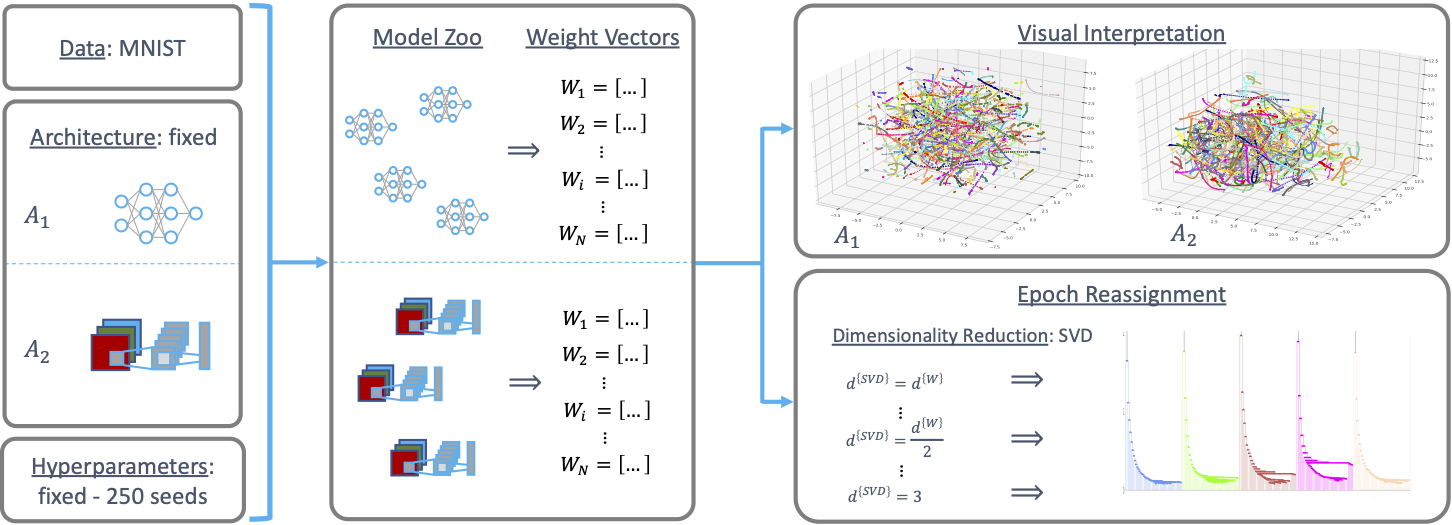
Experimental Setup

The approach of our work is outlined in the figure below. We first create a population of models with a fixed architecture and task, only varying the seed and thus initialization point in parameter space. By extracting the parameters or weights of the models, we can trace the development of models in the weight space.

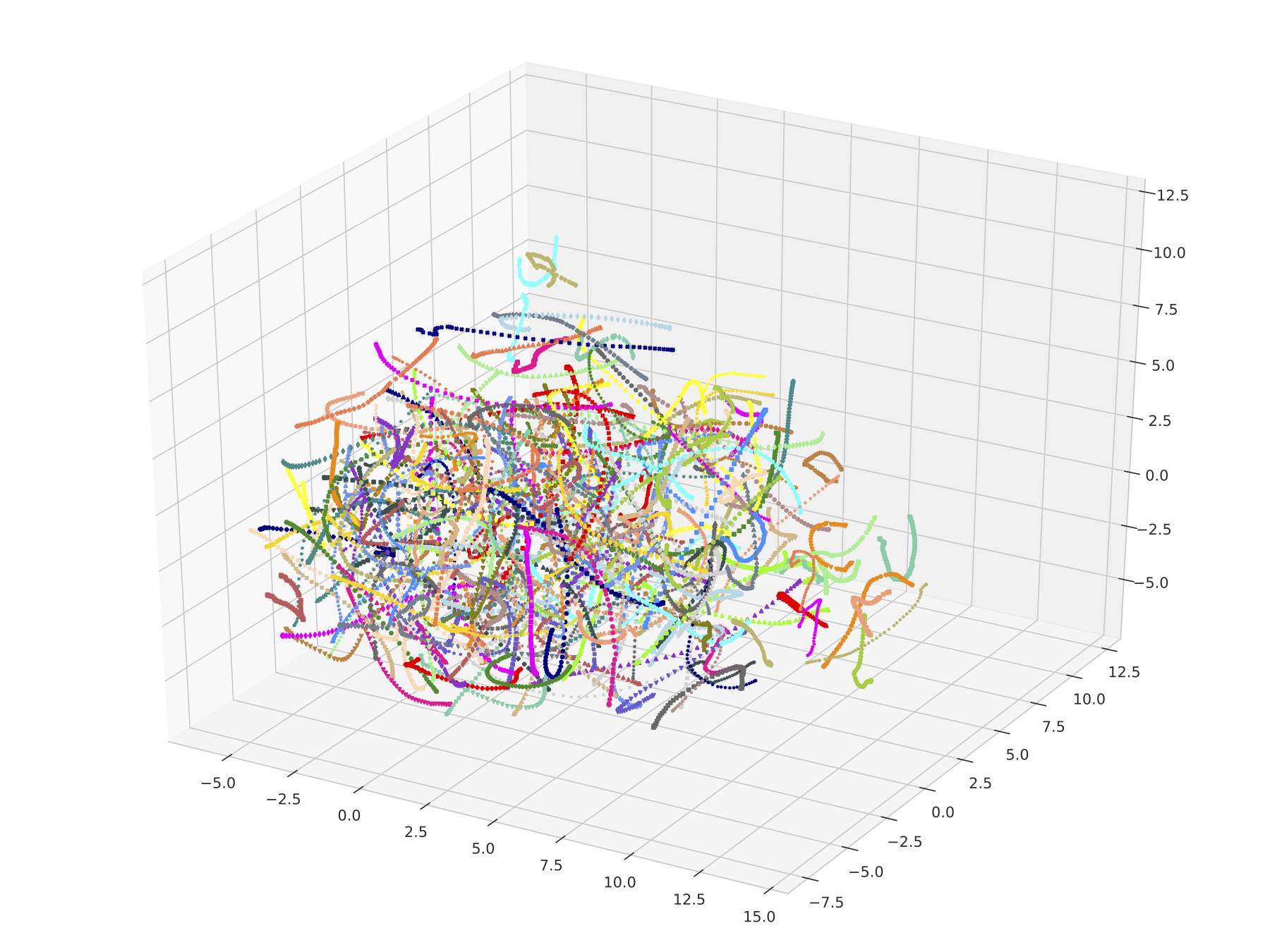
Qualitative Analysis

Applying dimensionality reduction methods to the high dimensional weight space allows for intuition on the trajectories. One example is shown in the figure below. The visualisation shows the distinct trajectories on which the models evolve. Further, the trajectories are smooth in the low-dimensional space. Lastly, they do not cross, the trajectories are unique and separable. alt text

Quantitative Analysis

To investigate these findings further, we investigated whether the trajectories can be recovered. To that end, we applied hierarchical clustering on the model samples in weight space. The results are visualized as a dendrogram in the Figure below. 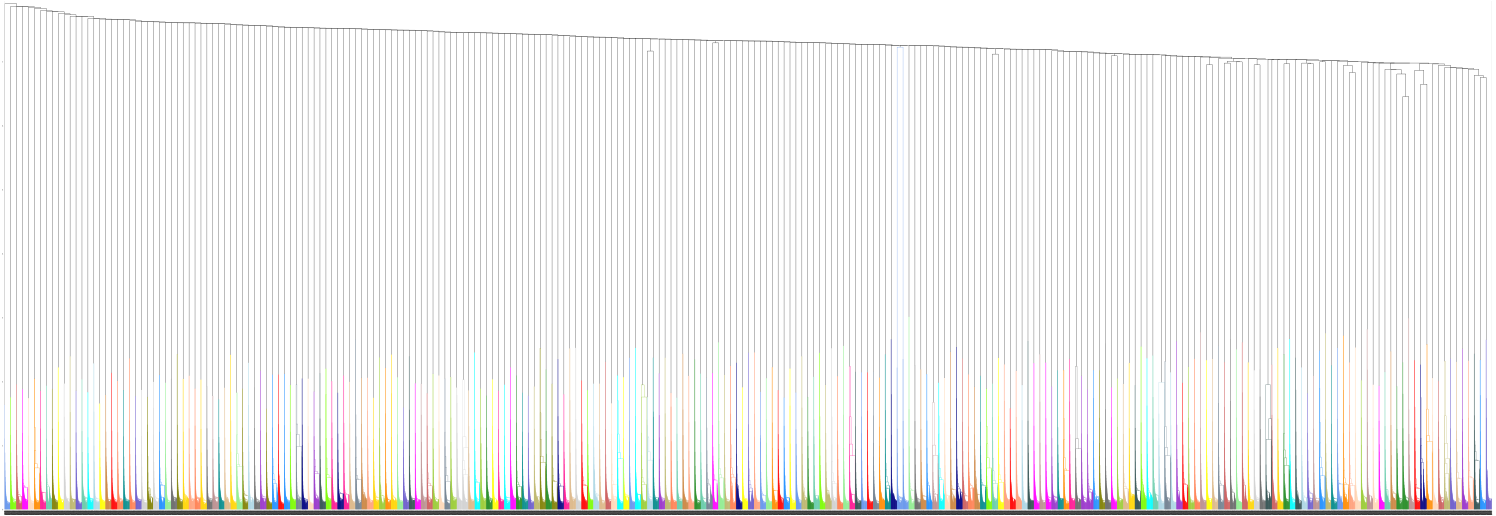alt text Here, different colours indicate different actual model trajectories. The dendrogram shows that the distance between model trajectories is always much larger than between checkpoints of the same trajectory.

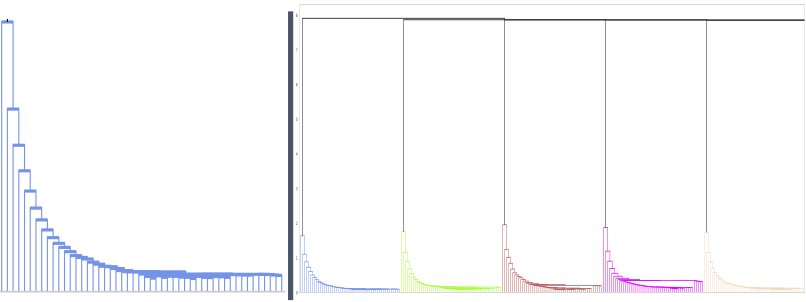
Further, the clusters often show a specific saw-tooth pattern, where the distance between individual samples on the trajectory reduce over training. As the update within one epoch directly relates to the training loss, the distance between checkpoints on the trajectory starts develops together with the loss. On the assumption of monotonically reducing loss and thus monotonously reducing distance between checkpoints, we can reconstruct the order of checkpoints in a cluster purely based on the distance. alt text

Outlook

This work takes the first step in investigating what properties of models are encoded in their parameter space. Future work will continue this line of work, with the goal of developing methods to monitor NN models during their training and facilitate NN model version control.